Algorytm – w matematyce skończony ciąg jasno zdefiniowanych czynności, koniecznych do wykonania pewnego rodzaju zadań. Słowo "algorytm" pochodzi od starego angielskiego słowa algorism, oznaczającego wykonywanie działań przy pomocy liczb arabskich (w odróżnieniu od abacism – przy pomocy abakusa), które z kolei wzięło się od nazwiska, które nosił Muhammad ibn Musa al-Chuwarizmi (أبو عبد الله محمد بن موسى الخوارزمي), matematyk perski z IX wieku.
Algorytm ma przeprowadzić system z pewnego stanu początkowego do pożądanego stanu końcowego. Badaniem algorytmów zajmuje się algorytmika. Algorytm może zostać zaimplementowany w postaci programu komputerowego.
Jako przykład stosowanego w życiu codziennym algorytmu podaje się często przepis kulinarny. Dla przykładu, aby ugotować bigos należy w określonej kolejności oraz odstępach czasowych (imperatyw czasowy) dodawać właściwe rodzaje kapusty i innych składników. Może istnieć kilka różnych przepisów dających na końcu bardzo podobną potrawę. Przykład ten ma wyłącznie charakter poglądowy, ponieważ język przepisów kulinarnych nie został jasno zdefiniowany. Algorytmy zwykle formułowane są w sposób ścisły w oparciu o język matematyki.
W niektórych krajach, jak USA, algorytmy mogą zostać opatentowane, jeżeli zostaną zaimplementowane w jakimś praktycznym celu. Niektórzy twierdzą, że patentowanie algorytmów spowalnia rozwój informatyki, bo jeden producent może uzyskać monopol, np. na pisanie oprogramowania tworzącego pewne typy plików(np. GIF). Wiele koncernów komputerowych prowadzi między sobą spory prawne dotyczące praw własności do niektórych patentów. Kontrargumentem jest tzw. prawo własności intelektualnej (jaką objęty jest np. utwór muzyczny, będący wytworem intelektu i pracy muzyka) zakładające, że program jest intelektualną własnością twórcy.
Przykład
Znalezienie największej wśród niepustej, nieposortowanej listy przypadkowych liczb można przeprowadzić na wiele sposobów, jednym z najszybszych jest przedstawiony niżej. Niech 
oznacza wskazuje aktualnie badany element listy (jeśli jest ona numerowana, może on oznaczać np. jej numer), a 
oznacza największą dotychczas znalezioną wartość.
- Niech wskazuje na pierwszy element (początek) listy.
- Niech zawiera wartość elementu listy wskazywanego przez (tzn. pierwszego).
- Jeżeli zawartość elementu listy wskazywanego przez jest większa od zawartości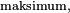
to przypisz wartość elementu wskazywanego przez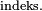 
- Niech wskazuje kolejny element listy; jeśli to niemożliwe (tzn. wskazuje ostatni element listy, czyli jej koniec), przejdź do punktu 6.
- Wróć do punktu 3.
- Koniec.
Wykonanie tego algorytmu spowoduje, że największa liczba na wspomnianej liście będzie wartością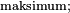 
ciekawostką jest fakt, iż algorytm ten działa dla list dowolnej długości (nie wykorzystuje on liczby elementów listy, lecz tylko tzw. operację następnika danej listy, tzn. przejścia do następnego jej elementu; niemożność wskazania kolejnego elementu jest wtedy równoważna temu, iż dany element jest ostatni na liście).